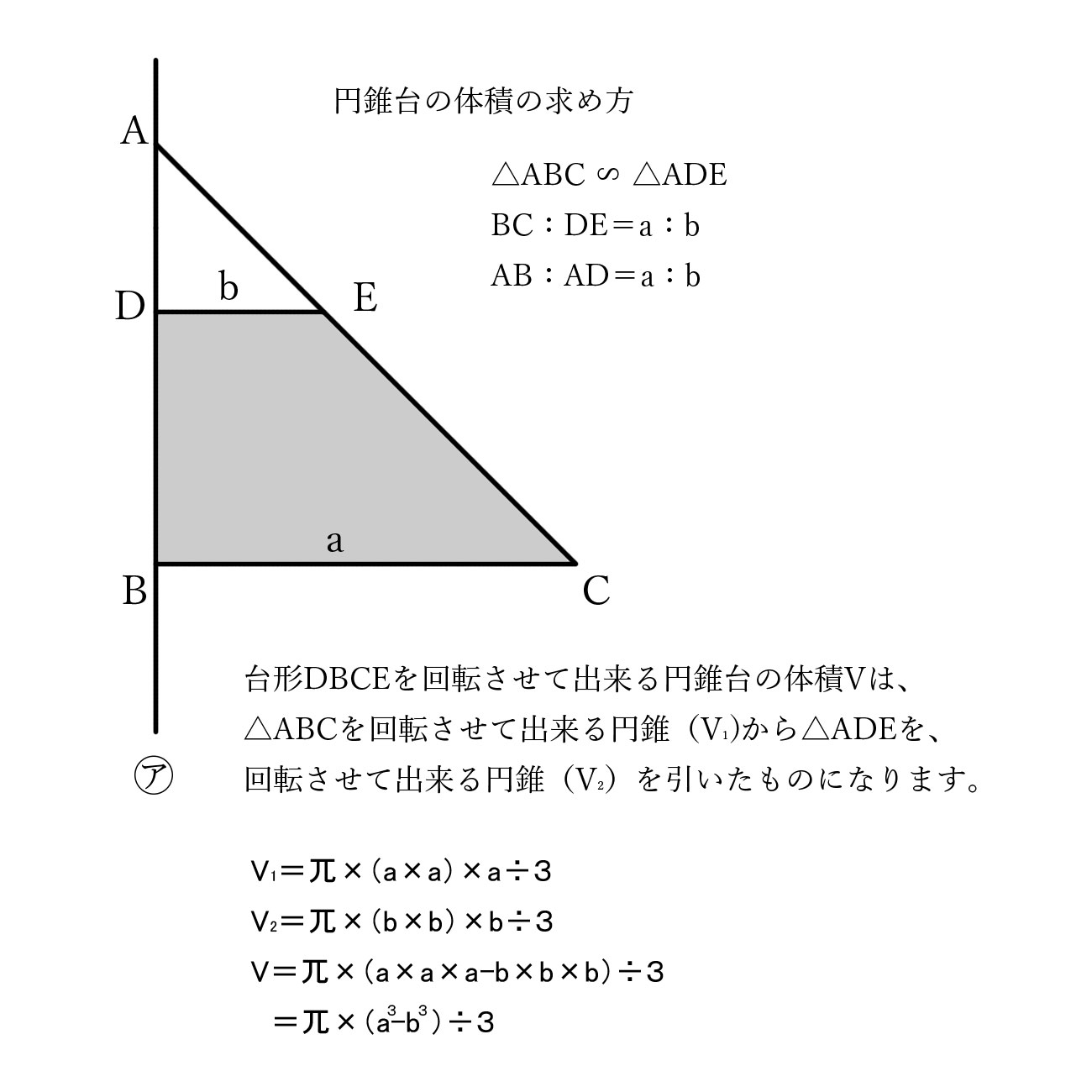
円錐は展開図にすると,円と扇形に分離されるのでこのような公式になります. 展開図がそのまま数式になっているので非常に分かりやすく理解しやすいと思います. 体積を求める公式 V = 1 3 π r 2 h V = 1 3 π r 2 h さて,次は円錐の体積を求める公式です.円柱の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円柱 円柱の体積を求める公式は、次の通りです。 V = Sh = πr2h V = S h = π r 2 h ここで、V は円柱の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の円の半径円錐 縦×横×高さ (半径)2×314×高さ 外径+内径×厚さ×314×高さ 2 (半径)3×314× 4 3 体積の計算式 (半径)2×314× 1 3 形 状 三 角 形 平行四辺形 台 形 半円筒形 立 方 体 円 錐 四 角 錐 平面形

円錐台 Wikipedia
円錐台 体積 求め方 小学生
円錐台 体積 求め方 小学生-円錐(すい)の表面積や側面となる扇形の面積と四角錐や五角錐の体積の求め方の説明です。 体積を求める公式はありますが、公式そのもので求める問題は多くありません。 立体では大切なポイントがありますので錐体の表面積や体積を求め くさび形の体積「上部の小さな円錐の高さは,相似比4:7から 比の差が3㎝→上部の高さは比の4だから4㎝」 の処理はちゃんとできるようになっていることが前提です。 一見ただの,円錐台の問題なのですが, 立式してみてください。



初等幾何 円錐台の側面積を求める 大人が学び直す数学
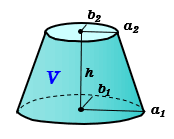
円錐台の体積の求め方を覚えましょう ≪円錐台の体積の求め方≫ 図bのように円錐を作り、以下の式で答えを求めます。 (大きな円錐)-(小さい円錐)=円錐台 図b 図bを見ると、小さい円錐の高さ(〇㎝)と大きな円錐の高さ(〇+4㎝)を求めることが相似比を3乗することで求めてやることができます。 つまり 相似比がわかれば 体積比はすーぐに求めることができるということですね! それでは、さっきの円錐の問題を考えてみましょう。 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるの円錐台の体積の求め方・まとめ 円錐台の体積を求めるときは、円の半径と高さを公式\(\frac{1}{3}\pi h(a^2abb^2)\)に代入しましょう。 円錐台の体積の求め方
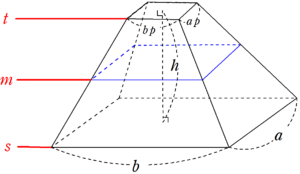
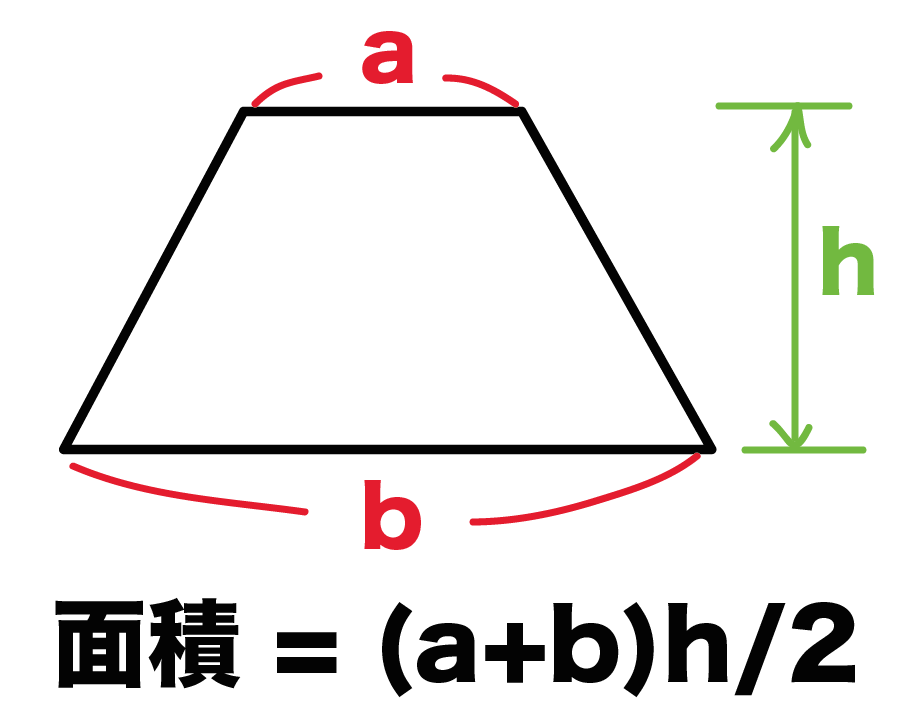
そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式!? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2)円錐の体積の公式を導こう。 x2 円錐の体積 半径r の円を底面とする高さh の円錐K を考える。底面積はS = ˇr2 である。 円錐K を高さの方向にn 等分する。j = 1;2; 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし
・円錐の体積の求め方 角錐や円錐の体積を出すとき、公式に当てはめるようにしましょう。最初に底面積を計算します。上図の円錐では、底面積は以下になります。 $3×3×π=9π$ その後、公式に代入して錐体の体積を出します。 $9π×4×\displaystyle\frac{1}{3}=12π$ 円錐の体積の求め方の公式って?? こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。 円錐の高さの求め方概要 円錐の高さを求める問題は、この2パターンくらいかな 母線と半径から、三平方の定理を使って求める 体積と半径から、円錐の体積の公式を使って求める 表面積と半径とかからも求められなくはないけど、複雑だから出ることは




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
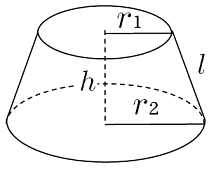
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S 楕円錐台の体積の求め方について 2251 円錐台の体積を求める公式はあるようですが、 楕円錐台の体積を求める公式というのはあるのでしょうか? また仮に、上面と下面の楕円の面積がわかっているとすれば、 その公式はどのようになります3点A,B,C を通る平面でこの立体を切ったとき、次のような立体の体積を求めなさい。ただし、点A,B,D は頂点、点C は辺の中点で、点A から点Dまで結ぶ辺は一直線になっています。 (1)小さい方の立方体で、この平面より下側の部分



1




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき、高さを求めてください。 円錐の高さは下式を用いて算定し円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の 円錐の体積を円柱座標系で真面目に計算してみた よく知られているように、円錐の体積は 1 3πR2h 1 3 π R 2 h です。 ここで底面の円の半径を R R 、高さを h h としました。 中学の数学などで天下り的に教わったのですが、導出は教わった記憶がありません




相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube



中学受験の問題です 分かりやすく解説 回答をお願いします 下の写真のような台形 Yahoo 知恵袋
円錐台 体積 求め方 円錐台 体積 求め方6− 1 3π ×22 ×3 = 28π v = 1 3 π ×円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も! 円錐を転がすと1周するのにどれくらい回転する? 円錐-円錐台 円錐を切り分けてできる円錐台の問題を解いてみましょう。 1. 図1のように、底面の半径が 3 cm、母線の長さが 12 cm の円錐があります。 このとき、次の(1)~(3)の各問いに答えてください。 (1) 円錐の側面となる扇形の中心角を求め;n に対して,頂点からの距離 が j n h である,底面と平行な平面で円錐K を切ったときの切口は



また来てね問題集 図形問題 解答と解説 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円錐の体積 円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。 円錐(えんすい、直円錐)とは? 円錐(えんすい)とは、 平面上の円の円周上の各点と、その平面上にない一点とを結んでできる立体。 中が空っぽの円錐は側面と底面の2つのパーツでできています。 中学の数学で勉強する円錐は、 底面の円の中心と頂点とを結ぶ線が、底面に垂直な直円錐




初等幾何 円錐台の側面積を求める 大人が学び直す数学




円錐の体積ってなんであの公式なの Webty Staff Blog
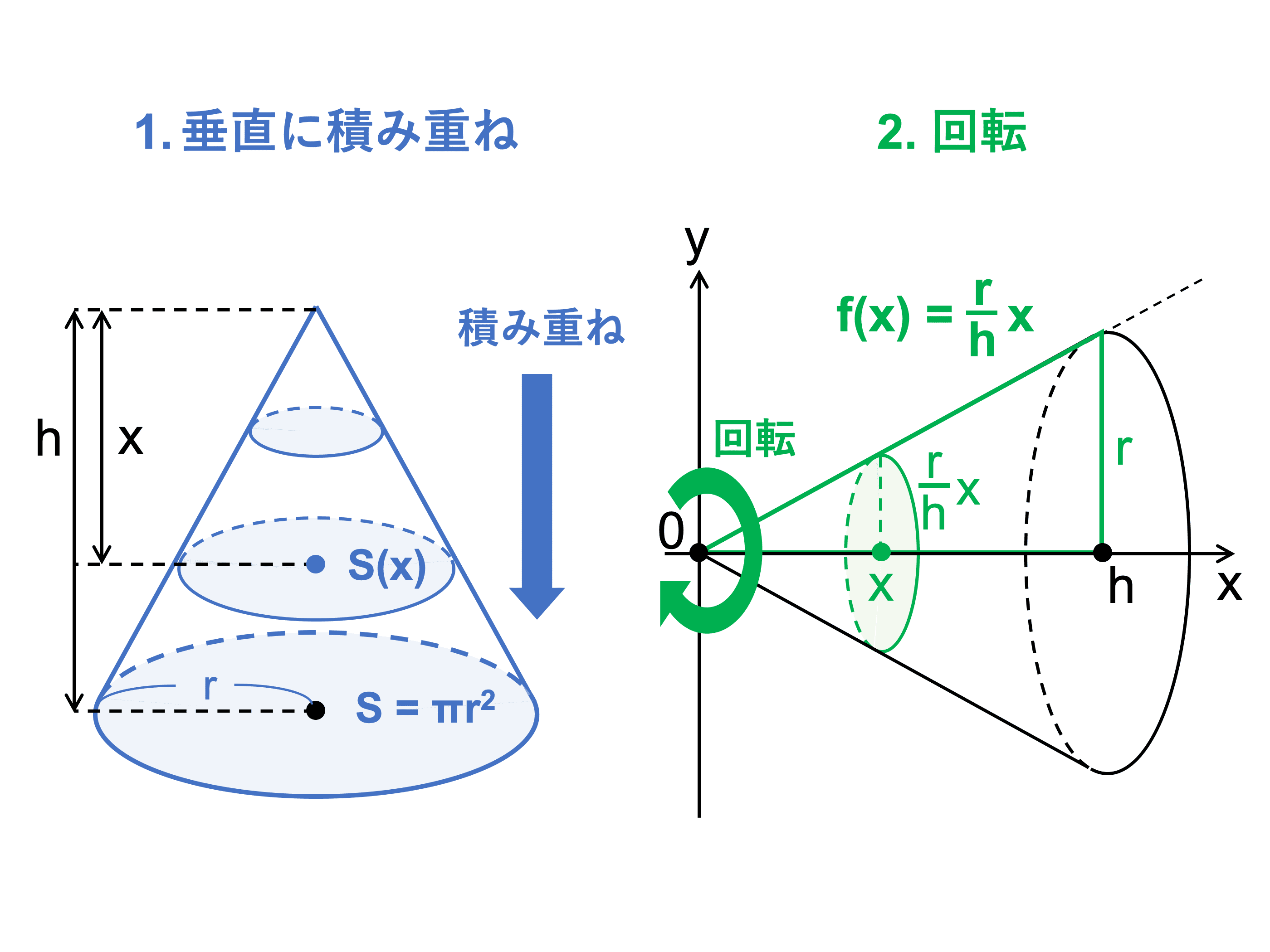
TikTokで円錐 体積求め方関連のショートムービーを探索しよう このクリエイターの人気コンテンツを見てみよう:かずおっち(@kazuocci), あきとんとん(@akitonton), あきとんとん(@akitonton), ゆーすけ@高校教師(@u_suke526), あきとんとん(@akitonton) ハッシュタグで最新動画を探索しよう:#円錐切除術, #円の 積分を用いて円錐の体積 を求める以下の公式を導出します. ここで, は底面の半径, は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角をθとすると,この直線は と表せます.この直線の式とx軸および2直線 および で囲まれた図形 おめでとう! まとめ:円錐の側面積の求め方は公式に頼らなくてもいい 球の体積、表面積 中学生にも納得のいく方法で。 半径3cm、母線9cmの円すいの表面積を求めなさい 裏ワザ公式を紹介する前にまずは通常のやり方でやってみます。 まずは底面積から。 円錐、角錐の表面積の公式は 底



円錐 台 表面積 円錐台の表面積の公式 Ofertadalu Com Br



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
本当にラストにします‥‥この底面の半径d高さhの円すいの重心位置を教えてください!式となんでその式になるかも教えてください!ANo4 の Tacosan の答えが常識なんですが教科書通り地道にやってみます。全体の重さを 1 とすると 密度は 今回は、円錐(えんすい)の体積の求め方(公式)について書いていきたいと思います。 // 円錐の体積の求め方公式 円錐の体積を求める問題 問題① 《円錐の体積の求め方》 問題② 《円錐の体積の求め方》 問題③ 《円錐の高さの求め方》 問題④ 《色のついた立体の体積の求め方》円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式 に当てはめて となるので、体積は となりました。 三平方の定理を使って 高さを求めることができれば あとは1年生で学習したこと




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




最も人気のある 三角 錐 体積 の 求め 方 ニスヌーピー 壁紙
円錐台(えんすいだい、英 circular truncated cone )は、底面が円である錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される立体である。 ある相似比27の三角錐では、体積比はいくつになるでしょうか。 解答 上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3:7^3=8:343と変換されました。 今度は逆に体積比から辺の長さの比を求めていきましょう 例題角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 このようなお悩みをもつ保護者の




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



小5の学習ポイント5 すい体と回転体 前田昌宏の中学受験が楽しくなる算数塾



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su
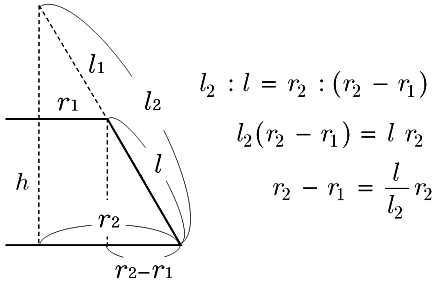



初等幾何 円錐台の側面積を求める 大人が学び直す数学
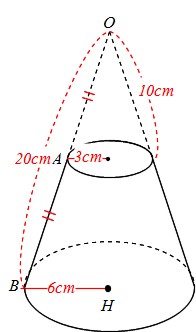



Math 円錐 円錐台と面積比 体積比 働きアリ




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
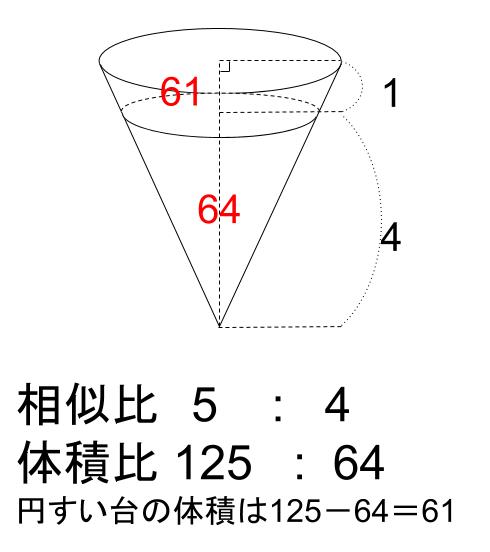



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




円錐台の問題がわかりません 写真は円錐の上部を底面に平行な平面で切った円 Okwave




円錐台を傾けた時に 溢れる水の体積の計算 上辺の半径r 下辺の半 数学 教えて Goo



円錐台の公式 体積 面積 数学 エクセルマニア




円錐 の 側 面積 の 求め 方 円錐となる回転体の側面積 表面積の求め方 中学1年数学 空間図形 Luismiguel Pt



1




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




M Sudo S Room 円錐台形の慣性モーメントに関する補足




マンスリーミニ対策 円錐台 中学受験 プロ家庭教師 コージー先生の独り言




ベスト 台形 の 体積 計算 1213 台形の体積 計算式 Nyosspixuugp




円錐の体積ってなんであの公式なの Webty Staff Blog



Studydoctor相似比と体積の計算 円錐台 三角錐台 中学3年数学 Studydoctor



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア



1



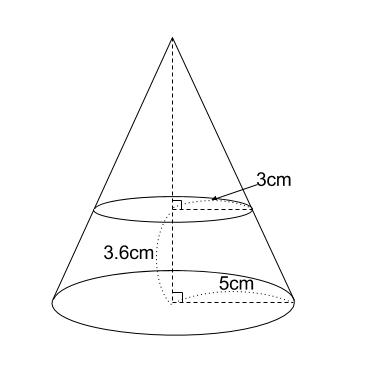
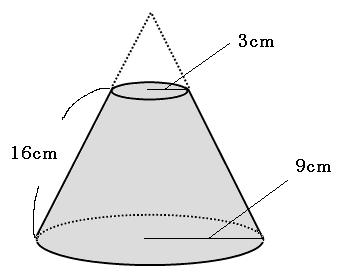
緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋
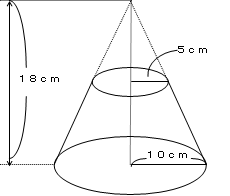



体積 円錐台の体積を求める 子供に教える算数のツボ




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




Solidworksで円錐台や円錐の作り方は



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



Newみんなの算数講座104 プリン 中学受験の算数知恵宝庫



Math 円錐 円錐台と面積比 体積比 働きアリ



シンプソンの公式 応用編 Fukusukeの数学めも




円錐台 Wikipedia




至急 3 を教えて下さい 答えは64 63 倍です Clearnote
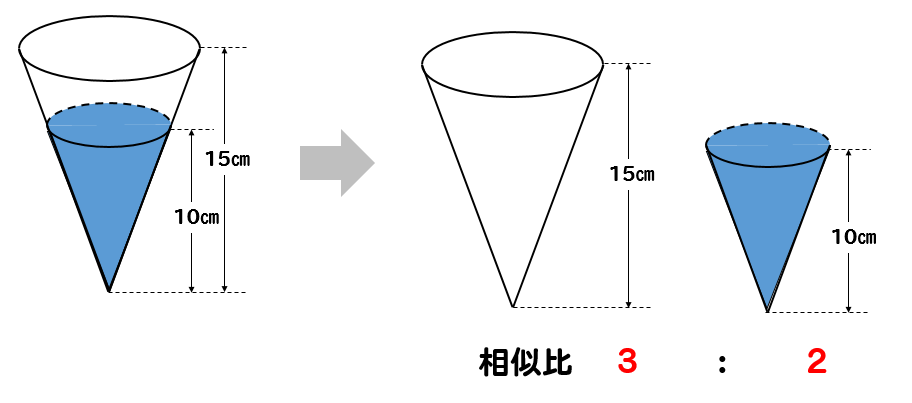



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




相似比と体積比 円錐台 中学3年数学 Youtube



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



地図の体積計測




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




体積の計算を教えてください 次の物体の体積がわかりません 計算方法から Okwave




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



楕円錐台の体積 高精度計算サイト
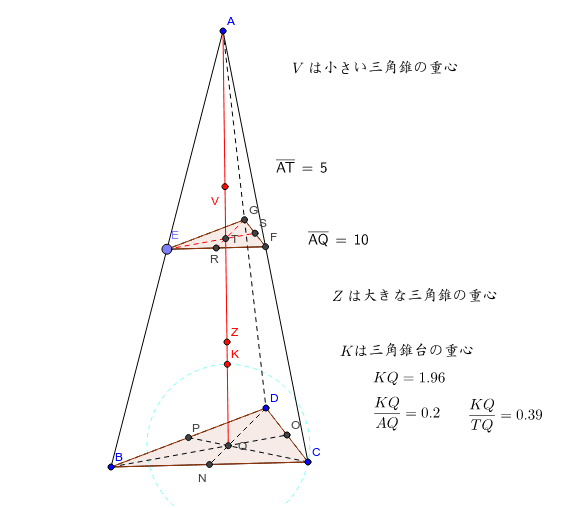



三角錐台の重心 Geogebra



私立中学 入試 問題の難問 偶然に 正解 セルフ塾のブログ




円錐を底辺に平行な2つの平面p Qで切断し 高さの等しい円錐aと円錐台 Okwave




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐台の体積の求め方円錐台の体積の求め方についての質問です 上 Yahoo 知恵袋



Mathematics 錐体の一部の体積 働きアリ




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




下の円錐台の体積の途中式まで教えていただきたいです Clearnote




ベスト 台形 の 体積 計算 1213 台形の体積 計算式 Nyosspixuugp



円すい台側面積の公式を導く



一般的なプリンの体積の求め方 地底たる謎の研究室
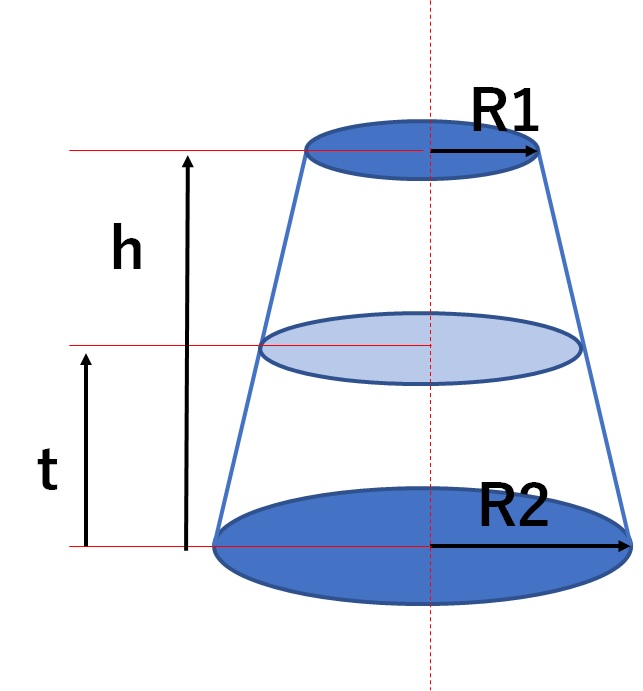



円錐台の体積を半分にする高さを計算 高精度計算サイト



頭の体操 問題3 解答 Cometのサボテン栽培日記




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ



円錐を カット する 体積は どうなる 名寄 算数数学教室より




円錐の体積の求め方 公式と計算例




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




Android 用の 体積計算 Bynsdev Apk をダウンロード




空間図形14 円すい台の体積 Youtube



Studydoctor相似比と体積比 円錐台 中学3年数学 Studydoctor



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐 台 表面積 円錐台の表面積の公式 Ofertadalu Com Br




円錐 の 体積 の 求め 方 円錐の体積の求め方 Ofertadalu Com Br



円錐 体積 求め方 積分 円錐 体積 求め方 積分 Jpdiamukpicttpfn
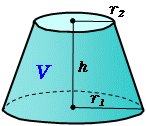



円錐台の体積 高精度計算サイト
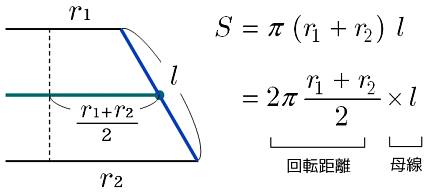



初等幾何 円錐台の側面積を求める 大人が学び直す数学



相似比と体積の計算 円錐台 三角錐台 中学3年数学 Youtube




円錐台の体積 側面積 香料ゐっすゐの夢



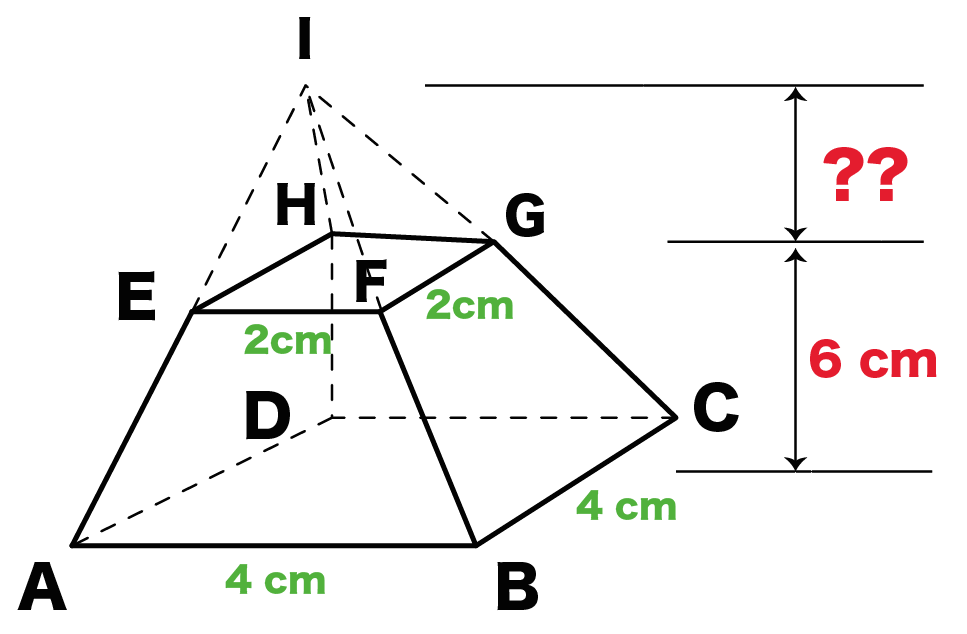
下のような四角錐台の体積の求め方をわかりやすく教えてください A 5b 3 Yahoo 知恵袋



添付写真は 円錐台に穴が開いているタイプの図形です この体積 Yahoo 知恵袋
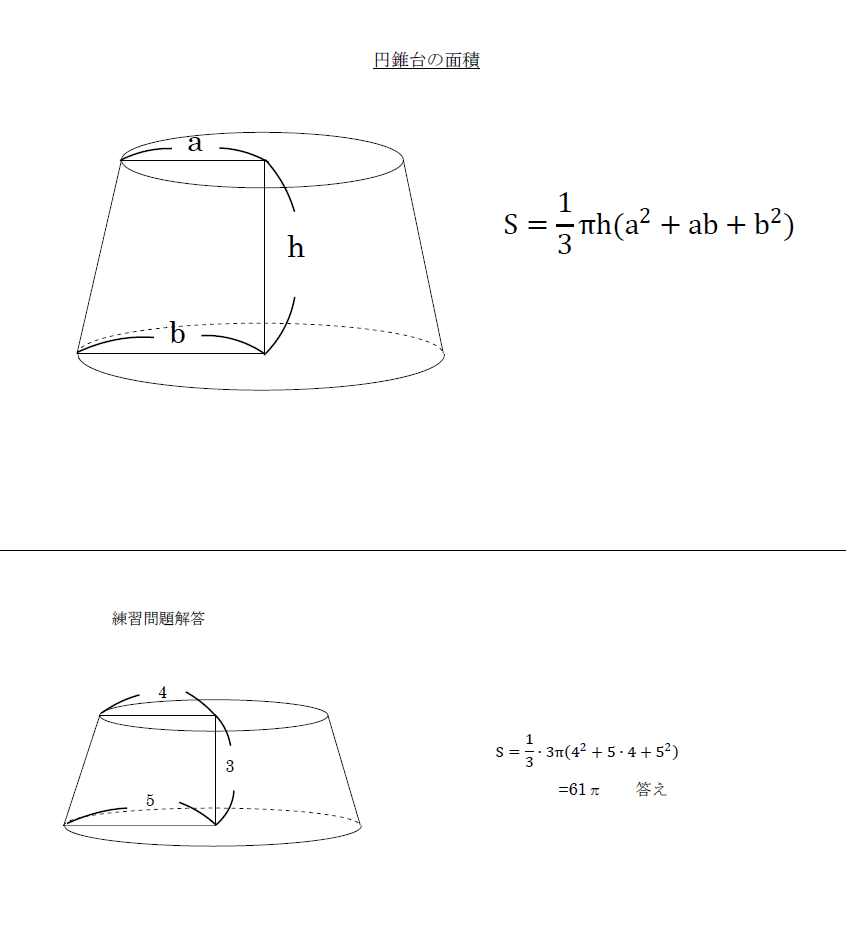



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法




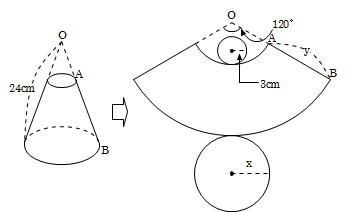
数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐 の 側 面積 の 求め 方 円錐となる回転体の側面積 表面積の求め方 中学1年数学 空間図形 Luismiguel Pt




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




高さの分からない円すい展開図 どうやって立体の体積を求めるの
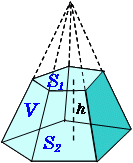



角錐台の体積 高精度計算サイト
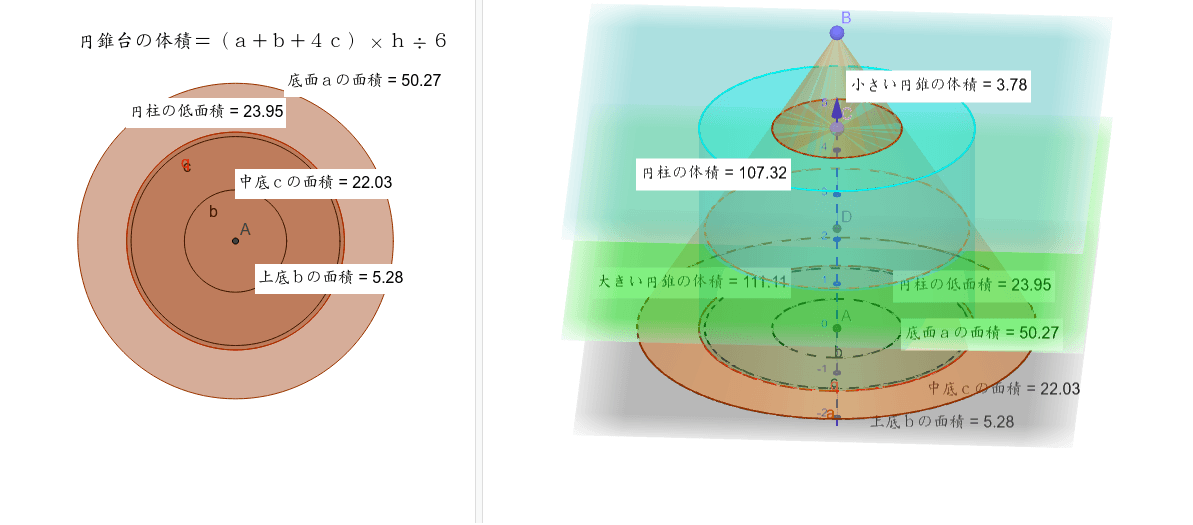



シンプソンの公式 Geogebra
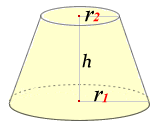



みんなの知識 ちょっと便利帳 円錐台の側面積を計算する



円錐 の 側 面積 の 求め 方 円錐となる回転体の側面積 表面積の求め方 中学1年数学 空間図形 Luismiguel Pt




解説お願いします Clearnote




50 素晴らしい角錐 体積 公式 ページを着色するだけ
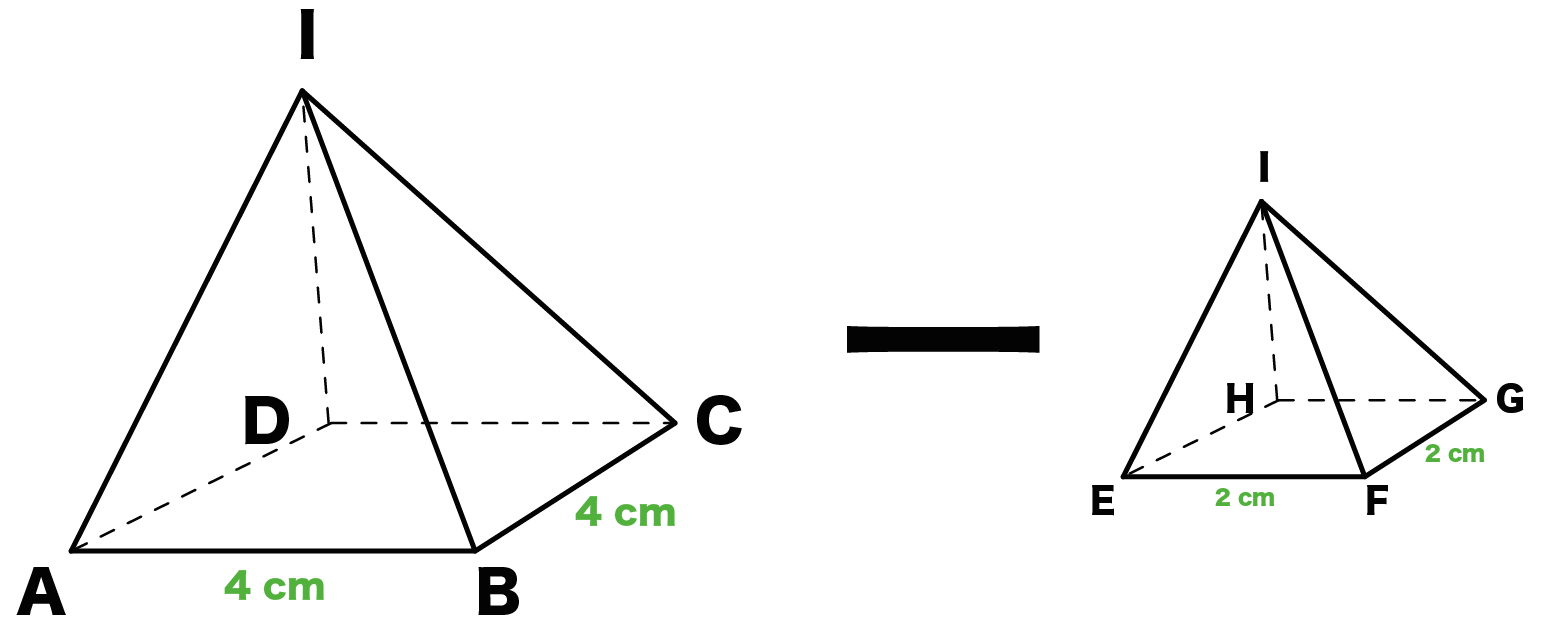



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




四角錐台の体積 高精度計算サイト




裏技 プリン型の立体の体積 一瞬で求められますか Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
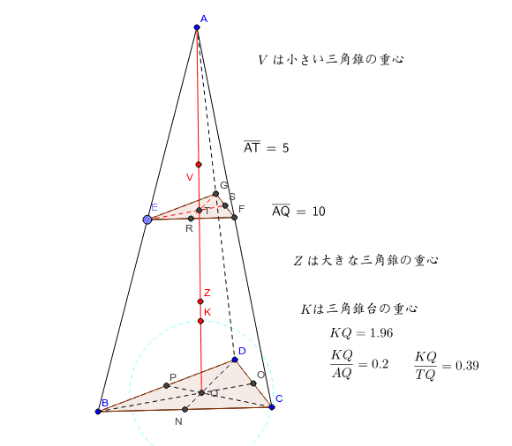



三角錐台の重心 Geogebra



1



0 件のコメント:
コメントを投稿